EXAMPLES

animations

	Velocity vector is always tangent to the path of motion. for circular motion this would be 90 degrees to the line between the object and the axis

centripetal force,, the ball would continue moving straight if the bottom of the can did not apply a force to it

on a roller coaster the forces at each position in the arc act in different directions

	forces felt by passengers in a car depend upon where they are sitting

Centrifugal Force - Turning a Bicycle

A bicycle held straight up will tend to go straight. It is tempting to say that it stabilized by the gyroscopic action of the bicycle wheels, but the gyroscopic action is quite small.	If the rider leans left, a torque will be produced which causes a counterclockwise precession of the bicycle wheel, tending to turn the bicycle to the left.

This is a good visual example of the directions of the angular momenta and torques, but the gyroscopic torques of bicycle wheels are apparently quite small (see Lowell and McKell). The gyroscopically motivated descriptions like "leaning left turns it left" are more appropriate to motorcycles.

If you lean left, you turn left

A rider leaning left will produce a torque which will cause the bicycle wheel to precess counterclockwise as seen from above, turning the bicycle left. The angulur momentum of the bicycle wheels is to the left. The torque produced by leaning is to the rear of the bicycle, as may be seen from the right-hand rule. This gives a rearward change in the angular momentum vector, turning the bicycle left.

This is a good visual example of the directions of the angular momenta and

Example: Rounding a curve

To see how we use the centripetal acceleration equation let's look at an example.

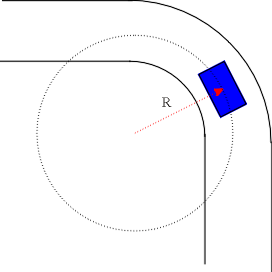
A car of mass m rounds a curve at a constant speed as shown below. The curve has a radius of curvature of R. (In other words, the curve is a piece of a circle of radius R.) If the coefficient of static friction between the road and the tires is m, what is the maximum speed the car can travel around the curve without slipping?

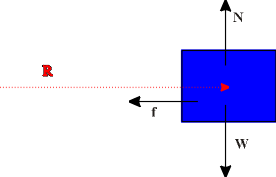
The free-body diagram of the car ( from a back view) is shown below.

In the vertical direction we find

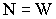
In the horizontal direction

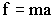
But we know that, (for maximum static friction),

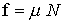
and

.

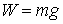In requirement that the car move in a circle allows us to use the centripetal acceleration formula.

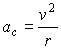
So putting it all together gives

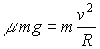
or, that the maximum velocity without slipping on the road is

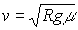
Notice that this expression has the right properties: the max velocity is reduced when the friction coefficient is reduced and the velocity is also reduced when the radius of the curve is reduced (making it a tighter turn).

Copyright © 2005 - S. B. EglI