| |
The following are the most common types of collision solutions
(note: these examples are from the
hyperphysics web site)
Elastic Collisions - Target Object Initially at Rest
 |
 |
Head-on Elastic Collisions
|
Velocities After Collision
may be used along with conservation of momentum equation
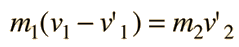
to obtain expressions for the individual velocities after the
collision.
|
| |
|
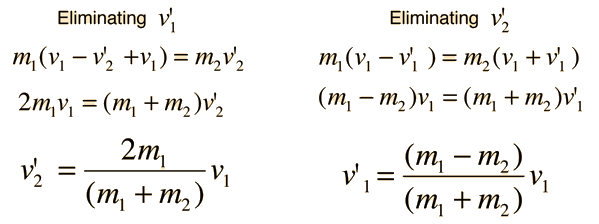
Head-on Elastic Collisions
 |
| |
|
Head-on Elastic Collisions
 |
| |
|
Elastic Collision, Equal Masses
For a head-on collision with a stationary object of
equal mass, the projectile will come to rest and the target will move off
with equal velocity, like a head-on shot with the cue ball on a pool
table. This may be generalized to say that for a head-on elastic collision
of equal masses, the velocities will always exchange.
|
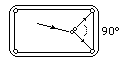
For a non-head-on elastic collision between equal
masses, the angle between the velocities after the collision will
always be 90 degrees. The spot on a pool table is placed so that a
collision with a ball on the spot which sends it to a corner pocket
will send the cue ball to the other corner pocket. |
 |
|
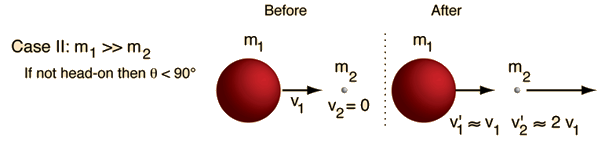
Elastic Collision, Massive Projectile
In a head-on
elastic
collision where the projectile is much more massive than the target,
the velocity of the target particle after the collision will be about
twice that of the projectile and the projectile velocity will be
essentially unchanged.
For non-head-on collisions, the angle between projectile and target is
always less than 90 degrees.
This case implies that a train moving at 60 miles/hr which hits a small
rock on the track could send that rock forward at 120 miles/hr if the
collision were head-on and perfectly elastic. It also implies that if the
speed of the head of your golf club is 110 miles/hr, the limiting speed on
the golf ball off the tee is 220 miles/hr in the ideal case. That is, the
limiting speed of the ball depends strictly on the clubhead speed, and not
on how much muscle power you put into the swing.
|
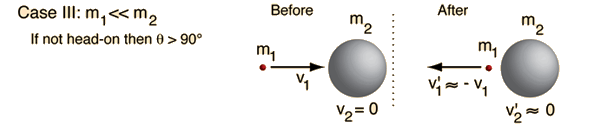
Elastic Collision, Massive Target
In a head-on elastic collision between a small projectile and a much
more massive target, the projectile will bounce back with essentially the
same speed and the massive target will be given a very small velocity. One
example is a ball bouncing back from the Earth when we throw it down.
In the case of a non-headon elastic collision, the angle of the
projectiles path after the collision will be more than 90 degrees away
from the targets motion.
|
Elastic Headon Collision
The head-on
elastic
collision relationships:
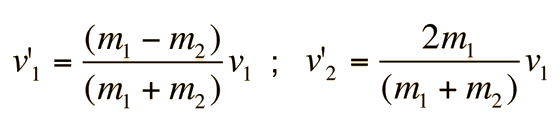
can be used to calculate the velocities resulting from
any such collision.
A positive velocity is taken as a velocity to the right
in the calculation, so for leftward motion you should enter a negative
number. The calculation assumes that a collision took place, but if you
get a negative number for the velocity of approach above, this means you
chose a scenario where no collision would actually happen.
|
Head-on Inelastic Collisions
In the general case of a one-dimensional collision between two masses,
one cannot anticipate how much
kinetic energy
will be lost in the collision. Therefore, the velocities of the two masses
after the collision are not completely determined by their velocities
before the collision. However,
conservation of momentum must be satisfied, so that if the velocity of
one of the particles after the collision is specified, the other is
determined.
For ordinary objects, the final kinetic energy will be less than the
initial value. The only way you can get an increase in kinetic energy is
if there is some kind of energy release triggered by the impact. Was one
of your objects a hand grenade?
|
Inelastic Collision Calculation
Most collisions between objects involve the loss of some kinetic energy
and are said to be inelastic. In the general case, the final velocities
are not determinable from just the initial velocities. If you know the
velocity of one object after the collision, you can determine the other
(see
inelastic head-on collisions). The extreme
inelastic
collision is one in which the colliding objects stick together after
the collision, and this case may be analyzed in general terms.
|
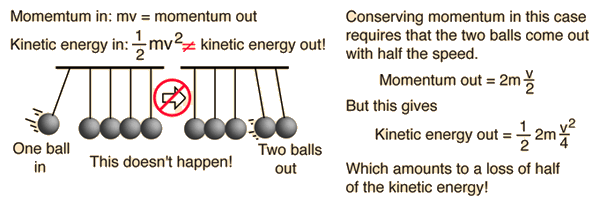
Swinging Balls
A popular demonstration of
conservation of momentum and
conservation of energy features several polished steel balls hung in a
straight line in contact with each other. If one is pulled back and
allowed to strike the line, one ball flies out the other end. If two balls
are sent in, two come out, and so forth.
|
|
