First, recall that objects resist linear
accelerations due to their mass - more mass means an object is more
difficult to accelerate. However, objects resist rotational
accelerations due to their rotational inertia (also called moment of
inertia) - more rotational inertia means the object is more difficult to
accelerate. Rotational inertia depends on:
- the object's mass - more mass means more rotational inertia, and
- how the object's mass is arranged relative to the axis of rotation -
if the mass is farther from the axis, you get more rotational inertia.
Suppose that you have several round objects that have the same mass and
radius, but made in different shapes. (This would be difficult in practice.)
The objects below are listed with the greatest rotational inertia first:
- a hoop - has the greatest rotational inertia, since all of its mass is
as far as possible from its axis (center).
- an empty can with no lid
- a hollow sphere - like a basketball, soccer ball, or volleyball
- a can of "sloshy" soup (chicken noodle) will have a higher rotational
inertia than a "solid" can because of the "sloshing" of the contents
- a can of "solid" soup (a cylinder)
- a solid sphere - like a billiard ball, has its mass packed as closely
as possible to its axis of rotation, so it has the least rotational
inertia
If you "race" these objects down the incline, they would definitely
not tie! This is because Newton's Second Law for Rotation says
that the rotational acceleration of an object equals the net torque on the
object divided by its rotational inertia. (Net torque replaces net force,
and rotational inertia replaces mass in "regular" Newton's Second Law.) The
net torque on every object would be the same - due to the weight of the
object acting through its center of gravity, but the rotational inertias are
different. This means that the solid sphere would beat the solid cylinder
(since it has a smaller rotational inertia), the solid cylinder would beat
the "sloshy" cylinder, etc. The hoop would come in last in every race, since
it has the greatest moment of inertia (resistance to rotational
acceleration).
Now, things get really interesting. What if you don't worry
about matching each object's mass and radius? In other words, you find any
old hoop, any hollow ball, any can of soup, etc., and race them. What
happens then? The result is surprising!
It turns out, that if you calculate the rotational acceleration of a
hoop, for instance, which equals (net torque)/(rotational inertia), both the
torque and the rotational inertia depend on the mass and radius of the hoop.
This means that both the mass and radius cancel in Newton's Second Law -
just like what happened in the falling and sliding situations above! (The
mathematical details are a little complex, but are shown in the table below)
This means that all hoops, regardless of size or mass, roll at the same rate
down the incline! The same is true for empty cans - all empty cans roll at
the same rate, regardless of size or mass. However, every empty can will
beat any hoop! All solid spheres roll with the same acceleration, but every
solid sphere, regardless of size or mass, will beat any solid cylinder!
Cool, huh? |
|
Now, the component of the object's
weight perpendicular to the radius is shown in the diagram at right. This
means that the torque on the object about the contact point is given by:
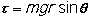
and the rotational acceleration of the object is:
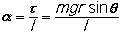
where I is the moment of inertia of the object. Now the moment of inertia
of the object = kmr2, where k is a constant that depends on how
the mass is distributed in the object - k is different for cylinders and
spheres, but is the same for all cylinders, and the same for all spheres.
The rotational acceleration, then is:
 
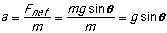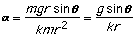
So, the rotational acceleration of the object does not depend on its
mass, but it does depend on its radius. However, we are really
interested in the linear acceleration of the object down the
ramp, and:
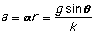
This result says that the linear acceleration of the object down the ramp
does not depend on the object's radius or mass, but it does depend on how
the mass is distributed. Therefore, all spheres have the same acceleration
on the ramp, and all cylinders have the same acceleration on the ramp, but a
sphere and a cylinder will have different accelerations, since their mass is
distributed differently. All spheres "beat" all cylinders. All cylinders
beat all hoops, etc. |
|
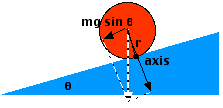
with the horizontal. The weight, mg, of the object exerts a torque through
the object's center of mass. The object rotates about its point of contact
with the ramp, so the length of the lever arm equals the radius of the
object.
