Review Questions

51) A common thread spool rests on a flat table. You gently pull in a horizontal direction on a short piece of thread attached to (wrapped around) the spool. Will the spool roll toward you if the string is wound over the top of the spool spindle? How about under the bottom of the spindle?

CLICK ON THUMBNAIL TO SEE DIAGRAM

p51a & b. Spool with thread over top (left) and over bottom (right) and co-linear with lever

each of the two on the left would cause rotation to the left, the third one would not rotate but would slide to the left because there is no perpendicular force to the lever arm

_{START
55 60 65
70 75 80
85 END}

52) Explain why a ball gains speed as it rolls down an incline in terms of torque. Now explain why in terms of forces.

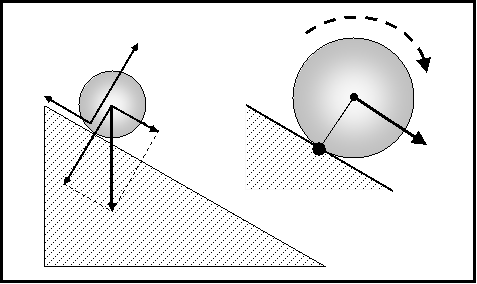Torque is created by the force of gravity acting on the center of the ball which is not over the contact point of support. This causes a Torque about the contact point resulting in an angular acceleration down the incline.

The parallel component of the force produced by gravity acting on the ball creates a torque around the contact point, resulting in rotation. Friction is essential for rotation to occur and its force is equal to the coefficient of friction multiplied by the normal component of the weight of the ball. Without friction the ball would slide down the incline rather than rotate.

53) A 4-kg ball is whirled on the end of a string that is 3 m long. The balls linear speed 2mis. What is its angular momentum?

Angular momentum = Rotational Inertia x Rotational Speed = mass x linear velocity x radius of rotation

= 4 kg x 3 m x 2 m/s = 24 kg - m^2/sec

Plug in the numbers for your answer!!

54) At the health spa, Felix Flex finds that pulleys on the exercise machines are not circular, but are “cams” -- sort of oval- shape. What do pulleys of this shape do to the length of the lever arms and the forces exerted by the machine?

CAM increases lever arm and multiplies the forces
CLICK FOR PICTURE

55) A common thread spool rests on a flat table. You gently puff at an angle on a short piece of thread attached to (wrapped around) the spool that causes the spool to slide without rotating. With the thread at this angle, the lever arm is

If no rotation occurs the net torque must be zero. Pulling at what angle from the lever arm would result in a net torque of zero? See picture for #51

_{START 55
60 65 70
75 80 85
END}

56) A meter stick is balanced at the 50-cm mark. You tie a 30-N weight at the 30-cm mark. Where should a 60-N weight be placed so the meter stick will again be balanced?

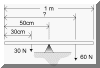CLICK ON THUMBNAIL FOR DIAGRAM

TRY the ANSWER OUT WITH THIS SIM !!!!!

*The hard way*	*An easier way*
ΣTorques =(30 N) x (.5 -.3 m) = (60 N) x (d - .5 m) ((30 N) x (.2 m) )/(60 N) = d -(.5 m) (.2m)/2 = .1 m = d -.5m (.1 + .5 )m = d d = .6 m = 60 cm mark	First move your origin to the fulcrum ΣTorques = 0 ((30 N) x .2 m)) - ( (60 N) x d_{from fulcrum}) = 0(30 N) x .2 m = (60 N) x (d_{from fulcrum})(30/60) x (.2m) = d_{from fulcrum}(.5) x (.2m) = d_{from fulcrum}d_{from fulcrum}= .1 to right of center or at the 60 cm mark

57) A ring, a disk, and a solid ball having equal masses roll down a hill at the same time. Which reaches the bottom first? Why?

click on thumbnail for picture

For why? and mathematical explanation go here

58) Suppose a carnival Ferris wheel has seats that are located halfway between the center and the outside rim. Compared to the ordinary Ferris wheel, where the seats are on the outside rim, would your linear speed be different? How about your angular speed?

Linear speed would be less, angular speed the same

59) When a gymnast moves from an extended position to a tucked position, how does her rotational inertia change?

Rotational Inertia is proportional to the square of the radius and dancers reduce their Inertia by tucking in their arms and/or legs. This increases their rotational speed through the conservation of Angular momentum = Rotational Inertia x Angular Velocity, The law of conservation of angular momentum tells us that decreasing their Rotational Inertia will increase their Angular Velocity (spin rate) To decrease Inertia they can pull their hands and arms into their body from an extended position. Gymnasts, skaters, skiers, dancers all do some variation of this to either increase of decrease their speed of rotation for specific moves. also tuck their knees into their chests while doing tumbling and other aerials. Same answer for questions #77, 59,64

60) Solid cylinders will roll down an incline with greater acceleration than hollow cylinders. What is the effect of mass and diameter on this? Is there some combination of diameter and mass that will result in a solid cylinder accelerating less?

No effect. No. mathematical explanation go here

_{START 55
60 65 70
75 80 85
END}

61) Which rolls to the bottom of a hill sooner, an empty car tire or same tire mounted on a rim?

A tire is a ring or hoop, with the wheel inside of it becomes a disk or cylinder. Tire on rim will be faster

For rest of answer see # 57.

62) A ring and a disk roll down a hill together which reaches the bottom first?

Disk. mathematical explanation go here

63) If the planet Jupiter underwent gravitational collapse, what would happen to its rate of rotation about its axis?

Radius decreases, what would the rotational speed do to maintain momentum

64) When an ice skater pulls in his hands while in a spin what happens to his moment of inertia? His angular momentum? His rotational speed?

Rotational Inertia is proportional to the square of the radius. Athletes and dancers reduce their Inertia by tucking in their arms and/or legs. This increases their rotational speed through the conservation of Angular momentum = Rotational Inertia x Angular Velocity, The law of conservation of angular momentum tells us that decreasing their Rotational Inertia will increase their Angular Velocity (spin rate) To decrease Inertia they can pull their hands and arms into their body from an extended position. Gymnasts, skaters, skiers, dancers all do some variation of this to either increase of decrease their speed of rotation for specific moves. also tuck their knees into their chests while doing tumbling and other aerials. Same answer for questions #77, 85, 59

65) Which has less rotational inertia, a girl running with her legs bent or the same girl running with her legs straight?

_{START 55 60
65 70 75
80 85 END}

66) Two people sit on a balanced seesaw. When one person leans toward the center of the seesaw, what happens to that person’s end of the seesaw? Why?

Decrease Torque and create imbalance making that person's end rotate up

67) The resistance an object has to changes in its rotational state of motion is called rotational______________

INERTIA click here for definition

68) If a football is kicked so the force on the ball is through its center of gravity, will the ball tumble or move without tumbling? Explain why.

In theory yes, but in reality, your foot is moving in a circular path and it would be impossible to follow through in a perfectly linear manner. If you see this on the exam the answer is still 'YES'

69) Will an object always change its angular momentum when acted on by an unbalanced force?

NO, only if that force produces a TORQUE

70) Which has more rotational inertia, a bicycle wheel or a solid disk of the same mass and diameter?

Bike wheel can be considered a hoop a solid disk is a cylinder.
For rest of answer and mathematical explanation go here For diagram go to #57

_{START 55
60 65 70
75 80 85
END}

71) Define angular momentum.

Rotational Inertia x Angular Velocity = mvr for concentrated mass. (ball on string, hoop)

click here for definition Hyperphysics - Angular Momentum

72) Which will roll down an incline with the greatest acceleration, objects with large rotational inertias or objects with small rotational inertias?

SMALL ROTATIONAL INERTIAS WILL BE FASTER IN GENERAL BUT IS ACTUALLY ROTATIONAL INERTIA PER UNIT MASS THAT DETERMINES

For solution & mathematical explanation go here

73) To turn a stubborn screw, it is best to use a screwdriver that has a long handle, or one that has a wide handle? Why?

probably at T-Handle or even better yet, a bit in a power driver!

74) Is a person’s rotational inertia is least about his longitudinal, transverse, or median axis?

LONGITUDINAL. Median and Transverse would be approximately equal.

Look in your book, section 11.5

CLICK FOR PICTURE

75) Suppose you try loosening a nut with a wrench, and the nut doesn’t give at all. Can you increase your chance of success if you use a longer wrench? If you exert a larger force? Make sure that you are pushing perpendicular to the wrench? Explain your reasoning in each case.

YES, more torque. YES, more torque. Yes, if force was not all perpendicular part of it was being wasted. Y

_{START
55 60 65
70 75 80
85 END}

76) Torque is defined as __________ Produce of Perpendicular force and length of lever arm

click here for definition HyperPhysics - Torque

77) Suppose a huge rotating cloud of particles in space gravitates together to form a dense ball. As the cloud shrinks in size what happens to its rate of rotation?

Angular momentum = Rotational Inertia x Angular Velocity, to conserve momentum (to keep it from changing), as the cloud gets smaller (its rotational inertia gets smaller) its Angular Velocity must increase

TRUE/FALSE. If true, mark “A”, If false, mark “B” on the Scantron

78) How can Ice skaters increase their spin rate by using the conservation of angular momentum?

Angular momentum = Rotational Inertia x Angular Velocity, conservation of angular momentum tells us that decreasing their Rotational Inertia will increase their Angular Velocity (spin rate) To decrease Inertia they can pull their hands and arms into their body from an extended position._

Skating video (avi 565 kb)

Skating Video (avi 850 Kb)

79) In order for a seesaw to be in rotational equilibrium, must the torques acting on it be balanced? Do the riders have to sit equidistant from the fulcrum ?

In other words if you weigh 150 pounds and another person weighs 100 pounds and you both sit at the same distance from the center of the seesaw will it be balanced (in rotational equilibrium)?

80) A spinning wheel will maintain its state of angular momentum unless acted on by what?

click here for law of conservation of angular momentum

_{START 55
60 65 70
75 80 85
END}

81) Define rotational inertia.

Property of an object or system use to quantify how it resists changes to its rotational state.

click here for definition

82) If you kick a football near one of its ends, will it tumble as it sails through the air? Why?

YES, You created a torque

83) Does a short pendulum have more rotational inertia than a long pendulum of the same mass? Explain.

Rotational Inertia for concentrated mass (weight at end of pendulum) is = mr²

84) Define torque

click here for definition

85) How can gymnasts change their rotational inertia while going through gymnastic routines?

86) Name two ways that a tightrope walker can increase his rotational inertia.

hold a long pole in your hands. Ever see a picture of one with a long bar in his hands. See Niagra Falls picture below.

click to see full size

87) What is the name of the distance between a turning axis and the point of contact of a perpendicular force?

LEVER ARM. click here if you still don't know

Chapter 11 Preliminary Assessment